GROUPES (mathématiques)Groupes finis

Née de l'étude des groupes de permutations des racines d'équations, la théorie des groupes finis s'est développée indépendamment depuis le Traité des substitutions et des équations algébriques (1870) de Camille Jordan. Après les travaux importants de Burnside, de Frobenius et de leurs élèves vers le commencement du xx^e siècle, cette théorie connut une période de développement lent, faute de méthodes pour résoudre les nombreux problèmes posés par ces pionniers. Les efforts de mathématiciens comme P. Hall et R. Brauer pendant cette période ont engendré les nouvelles méthodes qui, après 1955, ont amené une intense activité dans ce domaine ; des progrès énormes ont été accomplis, particulièrement dans la théorie des groupes simples et la théorie des relations entre un groupe et ses sous-groupes. Mais beaucoup de questions sont restées longtemps ouvertes et sont l'objet d'une recherche acharnée.

Groupes de permutations

Historiquement la théorie des groupes finis commença avec l'étude des groupes symétriques et de leurs sous-groupes, les groupes de permutations. Soit E un ensemble fini formé des n éléments e₁, ..., e_n, n ≥ 1. Une permutation π des éléments e₁, ..., e_n (ou encore une permutation π sur E) est une application x ↦ π(x) de E dans E, telle que chaque élément y de E soit l'image y = π(x) d'un élément unique x de E. L'application π^-1, envoyant chaque élément y sur l'élément x tel que y = π(x), est alors aussi une permutation sur E, qui s'appelle l'inverse de π. Le produit πρ de deux permutations π, ρ sur E est la permutation de e₁, ..., e_n définie par : πρ(x) = π(ρ(x)), pour tout x dans E. Avec ces définitions de l'inversion et de la multiplication, l'ensemble des permutations sur E forme un groupe fini Σ(E), le groupe symétrique de E. Son élément neutre est la permutation identité 1 = 1_E sur E, qui envoie chaque x = e₁, ..., e_n sur lui-même : 1_E(x) = x.

Le groupe symétrique Σ(E) est déterminé à un isomorphisme près par le nombre n = |E| d'éléments de E ; et on l'appelle souvent le groupe symétrique Σ_n de degré n, sans spécifier l'ensemble E. L'ordre | Σ_n | du groupe Σ_n, c'est-à-dire le nombre de ses éléments, est n ! = 1.2... (n − 1).n.

On peut représenter une permutation π de e₁, ..., e_n graphiquement par un tableau formé des éléments e₁, ..., e_n et de flèches. Chaque flèche joint un élément x = e₁, ..., e_n à son image y = π(x). Par exemple, si π est la permutation des éléments a, b, c, d, définie par π(a) = c, π(b) = a, π(c) = d, π(d) = b, son tableau est :

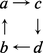
Une permutation comme celle-ci, dont le tableau a la forme d'une seule boucle, s'appelle une permutation cyclique. Elle se note en donnant les éléments dans leur ordre cyclique π = (a, c, d, b). Dans cette écriture, on peut commencer avec n'importe quel élément et écrire π sous les formes équivalentes :

Toute permutation sur E s'écrit comme un produit de permutations cycliques sur certains sous-ensembles de E. Ainsi, la permutation π de 1, 2, ..., 6 définie par : π(1) = 5, π(2) = 6, π(3) = 3, π(4) = 2, π(5) = 1, π(6) = 4, a pour tableau :

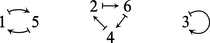
Il est évident que l'ensemble {1, 2, ..., 6} se décompose en une réunion disjointe des sous-ensembles {1, 5}, {2, 6, 4} et {3}, sur lesquels π opère comme les permutations cycliques (1, 5) (2, 6, 4) et (3). Ces permutations cycliques sont les cycles de π. La longueur d'un cycle de π est le nombre d'éléments dans le sous-ensemble correspondant. Donc π a des cycles de longueur 2, 3 et 1. On écrit π comme le produit (dans n'importe quel ordre) de ses cycles : π = (1, 5)(2, 6, 4) (3) = (4, 2, 6)(3)(1, 5) = ...

On a l'habitude de supprimer les cycles de longueur 1 quand l'ensemble E est connu. On écrit ainsi (1, 5)(2, 6, 4) au lieu de (1, 5)(2, 6, 4)(3) pour la permutation considérée précédemment. Cette notation est cohérente avec la notation adoptée pour la multiplication, car la permutation (1, 5)(2, 6, 4) = (1, 5)(2, 6, 4)(3) est en fait le produit des permutations (1, 5) = (1, 5)(2)(3)(4)(6) et (2, 6, 4) = (2, 6, 4)(1)(3)(5).

Si les longueurs des cycles d'une permutation π sont l₁, ..., l_k alors la signature sgn(π) de π est le nombre :

donc la signature de (1, 5)(2, 6, 4) est (− 1)^(2+3)+2 = − 1.

Si cette signature est égale à 1, la permutation π est paire, si elle est égale à − 1, elle est impaire. La fonction sgn est une fonction multiplicative : sgn(πρ) = sgn(π)sgn(ρ), pour toutes les permutation [...]

1  2  3  4  5 …
pour nos abonnés,
l’article se compose de 8 pages