GROUPES (mathématiques) Représentation linéaire des groupes
Théorie des représentations linéaires d'un groupe fini
La théorie classique trouvée par G. Frobenius, W. Burnside, et I. Schur dans la période 1890-1910 est la base de toutes les généralisations modernes. Cette théorie s'applique aux représentations linéaires d'un groupe fini G sur des espaces vectoriels de dimensions finies (c'est-à-dire ayant une base finie) sur le corps C des nombres complexes.
On cherche, d'abord, à classer les G-espaces, à des isomorphismes près. Un G-espace V est G-isomorphe à un G-espace U s'il existe une application linéaire bijective f de V sur U qui conserve les opérations de G : f (σv) = σf (v), pour tout σ dans G, et tout v dans V, c'est-à-dire si les représentations linéaires sont équivalentes.
L'outil principal de la classification des opérations linéaires de G sur des espaces vectoriels V est la décomposition des espaces V en somme directe de sous-espaces stables. Un sous-espace de V est un sous-ensemble U, qui est fermé pour la formation de combinaisons linéaires d'éléments ; U est donc lui-même un espace vectoriel avec, pour lois de composition, les restrictions des lois de composition de V. Le sous-espace U est stable par G s'il est fermé pour l'opération de G sur U, c'est-à-dire si σu appartient à U pour tout σ dans G et tout u dans U. Dans ce cas, la restriction à U de l'opération de G sur V est une opération linéaire de G sur U. Soit U1, ..., Uk des sous-espaces stables de V. On dit que V est la somme directe U1 ⊕ ... ⊕ Uk des Ui, si tout élément v de V a une expression unique de la forme :
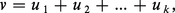
Les éléments u1, ..., uk sont les composantes de v pour la décomposition V = U1 ⊕ ... ⊕ Uk. La correspondance :
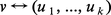
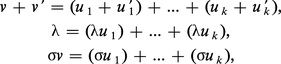
Si G opère sur un espace vectoriel U ≠ {0}, et s'il n'y a aucun sous-espace stable par G, sauf U et {0}, on dit que le G-espace U est irréductible. La classification des opérations linéaires d'un groupe fini G sur des espaces vectoriels V de dimension finie sur le corps C des nombres complexes est contenue dans les deux énoncés suivants : (3a) l'espace V a au moins une décomposition : V = U1 ⊕ ... ⊕ Uk, en somme directe de sous-espaces stables et irréductibles U1, ..., Uk ; (3b) si V = U′1 ⊕ ... ⊕ U′l est une autre telle décomposition, alors l = k et, après une permutation convenable des indices, Ui est G-isomorphe à U′i, pour i = 1, ..., k.
Pour tout G-espace irréductible W, on définit la multiplicité, m(W dans V), de W dans V. C'est le nombre des indices i = 1, ..., l pour lesquels W est G-isomorphe à Ui. À cause de (3 b), cette multiplicité est indépendante de la décomposition V = U1 ⊕ ... ⊕ Uk. Donc deux G-espaces V et V′ sont isomorphes si, et seulement si :

Frobenius découvrit une méthode très simple de calcul des multiplicités m(W dans V) en utilisant les caractères. On définit un produit hermitien (f |g)G sur l'espace vectoriel Fct(G, C) de toutes les fonctions de G dans C par :
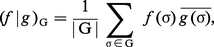
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
Écrit par
- Everett DADE : professeur à l'université de l'Illinois
Classification
Pour citer cet article
Everett DADE. GROUPES (mathématiques) - Représentation linéaire des groupes [en ligne]. In Encyclopædia Universalis. Disponible sur : (consulté le )
Autres références
-
ALGÈBRE
- Écrit par Jean-Luc VERLEY
- 7 143 mots
La structure de groupe est une des structures algébriques les plus simples et, sans conteste, la plus importante des mathématiques modernes. Son universalité ne s'arrête pas là : le psychologue Piaget a mis en évidence le rôle essentiel joué par cette notion dans les mécanismes mêmes de la pensée, et... -
ALGÉBRIQUES STRUCTURES
- Écrit par Jean-Marie PRUVOST-BEAURAIN
- 29 463 mots
Un groupe peut être défini indifféremment comme un monoïde (E, l) tel que tout élément de E soit symétrisable, ou comme un magma associatif unifère (E, l) tel que tout élément de E soit symétrisable, ou comme un groupoïde ayant un et un seul élément neutre. Tout semi-groupe fini est un groupe.... -
BOREL ARMAND (1923-2003)
- Écrit par Pierre CARTIER
- 795 mots
En 1992, le mathématicien Armand Borel a reçu le prix international Balzan « pour ses contributions fondamentales à la théorie des groupes de Lie, des groupes algébriques et des groupes arithmétiques, et pour son action inlassable en faveur de la recherche mathématique et de la propagation...
-
BURNSIDE WILLIAM SNOW (1852-1927)
- Écrit par Bernard PIRE
- 394 mots
Mathématicien britannique, spécialiste de la théorie des groupes. Né le 2 juillet 1852 à Londres (Grande-Bretagne) d'un père écossais, William Snow Burnside fait ses études supérieures au Pembroke College de l'université de Cambridge, dont il est diplômé en 1875 et où il effectue ses recherches...
- Afficher les 35 références
Voir aussi
- REPRÉSENTATION D'UN GROUPE
- OPÉRATION D'UN GROUPE
- GROUPES FINIS
- SOUS-GROUPE DISTINGUÉ OU NORMAL
- GROUPE SYMÉTRIQUE
- NORMALISATEUR
- FEIT & THOMPSON THÉORÈME DE
- PRODUIT HERMITIEN
- CARACTÈRE MODULAIRE
- CARACTÈRE, mathématiques
- TRACE, mathématiques
- GROUPE TOPOLOGIQUE
- TRIVIAL CARACTÈRE
- SOUS-ESPACE VECTORIEL
- SOMME DIRECTE
- REPRÉSENTATION LINÉAIRE DES GROUPES
- CARACTÈRE IRRÉDUCTIBLE
- ORTHOGONALITÉ


