SÉRIES ET PRODUITS INFINIS
La notion de limite d'une suite est à la base de l'analyse. Le langage des séries, équivalent à celui des suites, s'est imposé dès le xviie siècle à propos du développement des fonctions en série entière. Cependant, les fondements rigoureux de la théorie des séries, reposant sur une définition des limites, remontent seulement au début du xixe siècle, avec les travaux d'Abel, de Cauchy et de Gauss. L'étude des séries de nombres réels ou complexes et celle des séries de fonctions (séries entières, séries de Fourier, etc.) peuvent être considérées comme des cas particuliers de la théorie des séries d'éléments d'un espace vectoriel normé. On peut regrouper la notion de produit infini, utilisée par Euler au xviiie siècle, avec celle de série, à condition de se placer dans le cadre des groupes topologiques séparés.
Séries
Soit G un groupe commutatif topologique séparé, dont la loi est notée additivement. On appelle série d'éléments de G un couple A = ((un), (sn)) constitué de deux suites d'éléments de G telles que, pour tout entier naturel n, on ait :
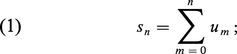
On dit que la série A est convergente ou divergente suivant que la suite (sn) converge ou non. Lorsque la série A est convergente, la limite s de (sn) s'appelle somme de A et se note encore :
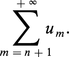
Il est immédiat que, si la série A converge, son terme général tend vers 0. Examinons les liens entre suites et séries. Pour toute suite (un) d'éléments de G, il existe une série A et une seule dont le terme général est (un) ; sa somme à l'ordre n est définie par la relation (1). Inversement, pour toute suite (sn) d'éléments de G, il existe une série A et une seule dont la suite des sommes partielles est (sn) ; son terme général est défini par les relations :
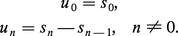
Ainsi, par définition, l'étude de la convergence d'une série se ramène à celle d'une suite. Réciproquement, les règles de convergence des séries peuvent servir à étudier la convergence d'une suite par l'intermédiaire de la série des différences.
Le cas fondamental dans la théorie des séries est celui où G est le groupe sous-jacent à un espace vectoriel normé E. Les séries d'éléments de E constituent un espace vectoriel ; les séries convergentes constituent un sous-espace vectoriel de l'espace vectoriel précédent, et l'application qui à toute série convergente fait correspondre sa somme est linéaire. La multiplication de Cauchy des séries d'éléments d'une algèbre normée ne présente d'intérêt que dans le cas des séries entières ; nous n'indiquerons ici que la multiplication des familles sommables (cf. infra).
Lorsque l'espace vectoriel normé E est complet, le critère de convergence de Cauchy prend la forme suivante : Pour qu'une série A = ((un), (sn)) converge, il faut et il suffit que, pour tout voisinage V de 0, il existe un entier naturel n0 tel que, pour tout couple (q, r) d'entiers naturels avec r > q ≥ n0, on ait :
Lien avec les intégrales impropres
Supposons toujours l'espace vectoriel normé E complet. L'étude de la convergence d'une intégrale impropre peut se ramener à celle d'une série, et réciproquement. Soit en effet f une application réglée (cf. calcul infinitésimal - Calcul à une variable, chap. 3) de [0, + ∞[ dans E admettant 0 pour limite à l'infini, (αn) une suite strictement croissante de nombres réels positifs tendant vers + ∞ telle que α0 = 0 et que la suite (αn+1 − αn) soit bornée,[...]
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
Écrit par
- Lucien CHAMBADAL : ancien élève de l'École normale supérieure, agrégé de l'Université, professeur au lycée Buffon, Paris
Classification
Autres références
-
BOREL ÉMILE (1871-1956)
- Écrit par Maurice FRÉCHET
- 2 290 mots
Sommation des séries divergentes.L'intervention fréquente des séries divergentes dans la théorie des fonctions analytiques, par exemple, conduisit Borel à rendre ces séries « convergentes » en un sens plus général ; dans son ouvrage Leçons sur les séries divergentes, il étudie divers... -
CALCUL INFINITÉSIMAL - Histoire
- Écrit par René TATON
- 11 465 mots
- 3 médias
Cet exemple nous conduit tout naturellement à signaler l'apport essentiel des années 1660, l'introduction systématique des séries infinies. Certes, l'intérêt porté aux algorithmes infinis apparaît dès l'Antiquité et se retrouve dans certaines spéculations scolastiques. Dès 1593, Viète avait développé... -
EULER LEONHARD (1707-1783)
- Écrit par Christian HOUZEL et Jean ITARD
- 2 759 mots
- 1 média
Euler était exceptionnellement doué pour le calcul, aussi bien numérique que formel. Dans l'Introductio, il manipule les séries et les produits infinis d'une façon prodigieuse et il trouve des résultats très remarquables, comme le développement de sin z en produit infini :qui lui donne...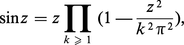
-
GAUSS CARL FRIEDRICH (1777-1855)
- Écrit par Pierre COSTABEL et Jean DIEUDONNÉ
- 4 886 mots
...avaient totalement négligé d'asseoir sur des bases solides leurs raisonnements de calcul infinitésimal et notamment n'hésitaient pas à calculer sur des séries divergentes, ils obtenaient d'ailleurs souvent ainsi des résultats exacts (pour des raisons qui nous sont maintenant claires mais ne pouvaient absolument... - Afficher les 13 références
