Universalis
Abonnez-vous à Universalis pour 1 euro

FONCTIONS ANALYTIQUES Représentation conforme

La représentation conforme la plus anciennement connue est la projection stéréographique, inventée par les Grecs (Hipparque, Ptolémée). Les problèmes cartographiques conduisirent à la découverte d'autres applications conservant les angles d'un domaine sphérique sur un domaine plan, telle la projection de Mercator (xvie siècle). Au début du xixe siècle, Carl Friedrich Gauss étudia systématiquement les propriétés intrinsèques des surfaces de l'espace habituel ; en particulier, il examina les applications bijectives d'une surface sur une autre qui sont différentiables, ainsi que leur réciproque, et qui conservent les angles. La notion de représentation conforme reçut un nouvel éclairage avec l'avènement de la théorie des fonctions d'une variable complexe, à laquelle elle est intimement liée. Bernhard Riemann sut exploiter cette relation de façon particulièrement féconde, introduisant la notion de surface de Riemann, qui résout les difficultés dues aux « fonctions multiformes » et donne un cadre convenable à la théorie du prolongement analytique. Cette théorie pose un certain nombre de problèmes topologiques qui ont conduit Bernhard Riemann et Henri Poincaré à développer les premières bases de la topologie algébrique.

Définition

La représentation conforme

Conservation des angles - crédits : Encyclopædia Universalis France

Conservation des angles

Encyclopædia Universalis France

Considérons un domaine D du plan R2. On dit qu'une application différentiable f de D dans R2 est conforme en un point z0 de D si sa dérivée (ou application linéaire tangente) D1 f (z0) en z0 conserve les angles orientés (cf. calcul infinitésimal – Calcul à plusieurs variables). En convenant que l'angle en z0 de deux chemins différentiables γ1 et γ2 passant par z0 est l'angle de leurs tangentes en z0, on voit que cette condition revient à la suivante : l'angle orienté en f (z0) des chemins images f ∘ γ1 et f ∘ γ2 est égal à l'angle orienté de γ1 et γ2 en z0, quels que soient les chemins γ1 et γ2 différentiables passant par z0.

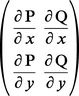
On sait qu'une application linéaire du plan dans lui-même, qui conserve les angles orientés est une similitude directe de centre O. Ainsi, la conformité de f en z0 signifie que l'application linéaire tangente D1f (z0) est une similitude directe. Il est très commode de représenter les similitudes à l'aide de la multiplication des nombres complexes. Dans la suite, on considérera que le plan est le corps des nombres complexes C, et l'on écrira x + iy pour le point (x, y) du plan (cf. nombrescomplexes) ; une similitude directe de centre O est alors une application de la forme z ↦ az, où a est un nombre complexe non nul dont le module et l'argument sont respectivement le rapport et l'angle de la similitude ; dans la base canonique (1, i) de C sur R, la matrice de la similitude considérée s'écrit :

où α est la partie réelle de a, et β sa partie imaginaire.

Dire que f est conforme en z0 revient donc à dire que sa dérivée est de la forme h ↦ ah, avec a ∈ C, a ≠ 0 ; par conséquent, le rapport :

tend vers 0 avec h, ou encore f est dérivable au sens complexe en z0, avec comme dérivée, f ′(z0) = a ≠ 0 (cf. fonctions analytiques – Fonctions analytiques d'une variable complexe, chap. 2). En termes réels, on doit écrire que la matrice jacobienne de f = P + iQ, soit :
est de la forme :
ce qui donne les conditions de Cauchy-Riemann :

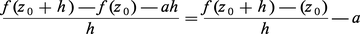
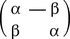
Ainsi toute fonction holomorphe f dans D, dont la dérivée ne s'annule pas, est conforme en tout point de D. Or on peut montrer que l'image d'une partie ouverte de C par une fonction holomorphe non constante est ouverte ; l'image du domaine D par une fonction holomorphe non constante f est donc un domaine f (D). De plus, si f est injective (on dit quelquefois univalente), sa dérivée ne s'annule pas ; f définit une bijection de D sur [...]

La suite de cet article est accessible aux abonnés

  • Des contenus variés, complets et fiables
  • Accessible sur tous les écrans
  • Pas de publicité

Découvrez nos offres

Déjà abonné ? Se connecter

Écrit par

  • : directeur de recherche au C.N.R.S., professeur à l'université de Paris-VIII-Denis-Diderot

Carte mentale
Élargissez votre recherche dans Universalis

Classification

Pour citer cet article

Christian HOUZEL. FONCTIONS ANALYTIQUES - Représentation conforme [en ligne]. In Encyclopædia Universalis. Disponible sur : (consulté le )

Médias

Conservation des angles - crédits : Encyclopædia Universalis France

Conservation des angles

Encyclopædia Universalis France

Représentation z &map; z<sup>2</sup> - crédits : Encyclopædia Universalis France

Représentation z ↦ z2

Encyclopædia Universalis France

Représentation z &map; z<sup>1/2</sup> - crédits : Encyclopædia Universalis France

Représentation z ↦ z1/2

Encyclopædia Universalis France

Afficher les 10 médias de l'article FONCTIONS ANALYTIQUES - Représentation conforme

Autres références

  • FONCTIONS ANALYTIQUES (A.-L. Cauchy)

    • Écrit par Bernard PIRE
    • 181 mots

    Augustin-Louis Cauchy (1789-1857) a écrit 789 notes qui furent publiées pour la plupart aux Comptes rendus de l'Académie des sciences. Parmi les nombreux résultats importants qu’il a démontrés, ceux qui concernent les fonctions d'une variable complexe ont marqué un tournant décisif dans l'histoire...

  • PRIX ABEL 2016

    • Écrit par Yves GAUTIER
    • 1 168 mots
    • 2 médias
    Pour ce qui est des formes modulaires, on peut dire très schématiquement que ce sont des fonctions analytiques qui respectent certaines conditions exprimées par certaines équations fonctionnelles – un exemple étant f[(az + b)/(cz + d)] = (cz + d)2 f(z) pour tout z complexe ; a, b, c et d étant...

  • ANALYSE MATHÉMATIQUE

    • Écrit par Jean DIEUDONNÉ
    • 8 527 mots
    ...exemple pour la fonction égale à exp (− 1/x2) pour x ≠ 0 et à 0 pour x = 0, en prenant x0 = 0). Il y a donc lieu de faire l'étude des fonctions, dites analytiques, qui, au voisinage de chaque point x0 où elles sont définies, sont égales à leur série de Taylor en ce point. On savait depuis...

  • ANNEAUX & ALGÈBRES

    • Écrit par Jean-Luc VERLEY
    • 5 036 mots
    • 1 média
    ...fonctions analytiques à l'origine O du plan complexe. Considérons les couples (U, f ) d'un voisinage ouvert de O dans le plan complexe et d'une fonction f définie et analytique dans U. Nous dirons que deux tels couples (U, f ) et (V, g) définissent le même germe à l'origine si f et ...

  • ASYMPTOTIQUES CALCULS

    • Écrit par Jean-Louis OVAERT, Jean-Luc VERLEY
    • 6 250 mots
    • 1 média
    Développements asymptotiques - crédits : Encyclopædia Universalis France
    ...) = etReh(x+iy), appelé le relief de eth(z). Cette surface ne présente pas de « sommet » relatif, d'après le principe du maximum pour les fonctions analytiques, et, par suite, les seuls points où le plan tangent est horizontal (ce sont les points où la dérivée h′(z) s'annule), sont...
  • Afficher les 20 références

Voir aussi

Abonnez-vous à Universalis pour 1 euro

Rejoignez-nous

Inscrivez-vous à notre newsletter