DÉRIVÉES PARTIELLES (ÉQUATIONS AUX) Théorie linéaire
Il existe une théorie mathématique assez bien constituée des équations aux dérivées partielles linéaires, dont nous allons essayer de donner une idée. En contraste, les équations non linéaires présentent un foisonnement de problèmes et de méthodes dont peu sont générales. Sans que nous le précisions à chaque fois, certains des résultats que nous allons donner dans le cas linéaire se généralisent au non linéaire. Pourtant, même ceux-là font partie de la théorie linéaire, soit que la généralisation non linéaire soit limitée à des situations trop restrictives, soit qu'elle ne s'insère pas dans une théorie cohérente.
Pour pouvoir conserver les notations de la partie précédente pour les problèmes d'évolution, nous nous placerons sur un ouvert de Rn+1 (à l'occasion Cn+1) et nous noterons en général y = (y0, y1,..., yn) les coordonnées. Pour α ∈ Nn+1, nous poserons :
Un opérateur linéaire aux dérivées partielles (on dit plus brièvementopérateur différentiel) est défini par un polynôme à coefficients pouvant dépendre de y :
À côté de ces notations, il nous arrivera d'utiliser des notations en (t, x) où t ∈ R (ou C) et x ∈ Rn (ou Cn) avec des conventions analogues pour les multi-indices, puissances et dérivations.
Nous ne nous priverons pas à l'occasion de noter les distributions comme des fonctions et les produits scalaires fonctions-distributions comme des intégrales (cf. distributions).
Le théorème de Cauchy-Kovalevskaïa
Supposons l'opérateur P de la forme :
Le problème de Cauchy s'énonce alors : « Trouver u vérifiant :
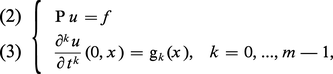
Le théorème de Cauchy-KovalevskaÎa suppose que les coefficients de P ainsi que les données f, g0, ..., gm-1 sont des fonctions analytiques (réelles ou complexes) de t et de x. Il affirme alors l'existence d'une solution analytique et une seule sur un voisinage de tout point (0, x0). Ce voisinage dépend de P et des domaines d'analyticité complexes des données.
Ce théorème s'applique aussi aux systèmes, pourvu qu'ils soient de la forme :
Le travail de Sofia Kovalevskaïa est paru en 1874 ; apparemment elle ne connaissait pas celui de Cauchy (et son jury non plus puisqu'il s'agissait d'une thèse !).
La démonstration d'unicité est simple et instructive. Si u est une solution analytique, elle possède un développement de Taylor en t :
La démonstration d'existence consiste essentiellement à démontrer la convergence de la série ainsi calculée. Elle repose sur une technique de majoration établie par Cauchy à cette occasion (méthode des séries majorantes).
La même démonstration s'applique d'ailleurs au système non linéaire (4) moyennant des complications légères.
Unicité de la solution distribution[...]
La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
Écrit par
- Martin ZERNER : professeur à l'université de Nice
Classification
Autres références
-
ANALYSE MATHÉMATIQUE
- Écrit par Jean DIEUDONNÉ
- 8 528 mots
...problèmes de mécanique, d'astronomie ou de physique. Au cours du xviiie siècle, les développements des applications des mathématiques à la physique avaient introduit des équations auxdérivées partielles, qui apparaissent aussi par ailleurs dans les problèmes de la naissante théorie des surfaces. -
CAFFARELLI LUIS (1948- )
- Écrit par Bernard PIRE
- 1 254 mots
- 1 média
Le mathématicien argentino-américain Luis Caffarelli a reçu le prix Abel – l'équivalent du prix Nobel pour les mathématiques – en 2023, pour « ses contributions essentielles à la théorie des régularités des équations aux dérivées partielles non linéaires ».
-
CALCUL INFINITÉSIMAL - Histoire
- Écrit par René TATON
- 11 465 mots
- 3 médias
En 1747, à l'occasion d'une étude sur le problème des vents, d'Alembert introduisit et étudia des équations d'un type nouveau, les équations aux dérivées partielles, faisant intervenir simultanément les dérivées partielles d'une même fonction par rapport à différentes variables. Le fait que la plupart... -
CAUCHY AUGUSTIN-LOUIS (1789-1857)
- Écrit par Jean DIEUDONNÉ
- 1 402 mots
- 1 média
...pures et appliquées. Si son œuvre en astronomie et en optique est secondaire, il est un des fondateurs de la théorie mathématique de l'élasticité. En analyse, il introduit la notion fondamentale de caractéristique dans la théorie des équations aux dérivées partielles du premier ordre, et il avait... - Afficher les 34 références
