NOMBRES (THÉORIE DES) Nombres p-adiques
On peut aborder l'étude d'un problème diophantien (cf. équations diophantiennes) en commençant par chercher les solutions modulo p, un nombre premier quelconque : on est alors devant un problème plus facile, car Z/pZ est un corps. Cette méthode ne donne qu'une information insuffisante pour le problème initial ; on la raffine en étudiant les équations modulo pm pour tous les entiers m ≥ 1. L'anneau Z/pmZ n'est pas un corps, mais ses propriétés arithmétiques sont beaucoup plus simples que celles de Z : c'est un anneau fini qui a un seul idéal premier (engendré par la classe de p) ; les autres idéaux sont les puissances de l'idéal premier.
Supposons maintenant qu'on connaisse une solution xm ∈ Z/pmZ du problème modulo pm ; pour tout k ≤ m, on en déduit une solution xk mod pk au moyen de l'application canonique évidente :
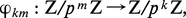
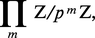
Généralités
Le noyau de l'homomorphisme canonique Z → Zp est formé des entiers divisibles par toutes les puissances de p ; il est donc réduit à {0}, et l'homomorphisme considéré est injectif et permet d'identifier Z à un sous-anneau de Zp. La surjection canonique Z → Z/pnZ se décompose en l'injection de Z dans Zp suivie de la projection de Zp dans le facteur Z/pnZ ; on voit ainsi que cette dernière projection est surjective ; son noyau est l'ensemble des entiers p-adiques (xm) tels que xn = 0, ce qui donne xm = 0 pour m ≤ n et xm ∈ pnZ/pmZ pour m > n ; autrement dit, ce noyau est l'ensemble des entiers p-adiques multiples de pn. On obtient ainsi l'isomorphisme :
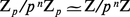
Pour n = 1, cela montre que Zp/pZp est un corps, donc que l'idéal pZp engendré par p est maximal. Si un entier p-adique x = (xm) n'appartient pas à pZp, chacune de ses composantes xm est inversible dans le facteur correspondant Z/pmZ et (xm-1) est inverse de x dans Zp ; ainsi l'idéal maximal pZp est exactement l'ensemble des éléments non inversibles de Zp, et c'est donc le seul idéal maximal : l'anneau Zp est local et son corps résiduel est Zp/pZp ≃ Fp, corps à p éléments. Les puissances successives de l'idéal maximal forment une suite décroissante (pmZp) d'idéaux dont l'intersection est visiblement {0} ; le plus grand de ces idéaux est p0Zp = Zp. La multiplication par pn est injective dans Zp ; il suffit de le vérifier pour n = 1, et px = 0 équivaut à pxm = 0 dans Z/pmZ pour tout m, ce qui donne :
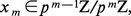

La suite de cet article est accessible aux abonnés
- Des contenus variés, complets et fiables
- Accessible sur tous les écrans
- Pas de publicité
Déjà abonné ? Se connecter
Écrit par
- Christian HOUZEL : directeur de recherche au C.N.R.S., professeur à l'université de Paris-VIII-Denis-Diderot
. In Encyclopædia Universalis []. Disponible sur : (consulté le )
Autres références
-
PRIX ABEL 2016
- Écrit par Yves GAUTIER
- 1 168 mots
- 2 médias
Le 15 mars 2016, l’Académie norvégienne des sciences et des lettres a décerné le prix Abel 2016 au mathématicien anglais Andrew John Wiles « pour avoir démontré de manière éclatante le dernier théorème de Fermat par le biais de la conjecture de modularité pour les courbes elliptiques semi-stables,...
-
ARITHMÉTIQUES (Diophante)
- Écrit par Bernard PIRE
- 188 mots
Diophante d'Alexandrie, parfois appelé le « père de l'algèbre », est connu par son ouvrage les Arithmétiques, qui traite des solutions des équations algébriques. On ne sait pratiquement rien de sa vie et ses dates de naissance et de mort sont très controversées. Les Arithmétiques...
-
ARTIN EMIL (1898-1962)
- Écrit par Jean-Luc VERLEY
- 1 319 mots
La part la plus importante de l'œuvre d'Artin concerne l'étude des corps de nombres algébriques etl'application des résultats obtenus à la théorie des nombres. Pour tout corps de nombres algébriques K, on peut considérer une fonction ζk(s), appelée la fonction zêta de Dedekind, qui... -
BAKER ALAN (1939-2018)
- Écrit par Bernard PIRE
- 338 mots
Alan Baker, mathématicien britannique, lauréat de la médaille Fields en 1970 pour ses travaux en théorie des nombres, est né le 19 août 1939 à Londres. Il a fait ses études supérieures à l'University College de Londres puis au Trinity College de Cambridge où il soutient sa thèse de doctorat en...
- Afficher les 56 références
Voir aussi


